To download and try this offline- CLICK HERE
To check answer- CLICK HERE
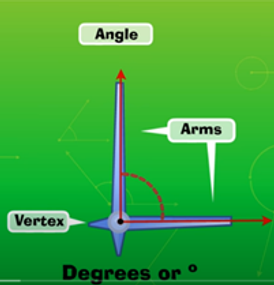
An angle is formed when two rays diverge from a common point.
The rays forming an angle are called the arms of the angle and the common point is called the vertex of the angle.
It is measured using a protractor.

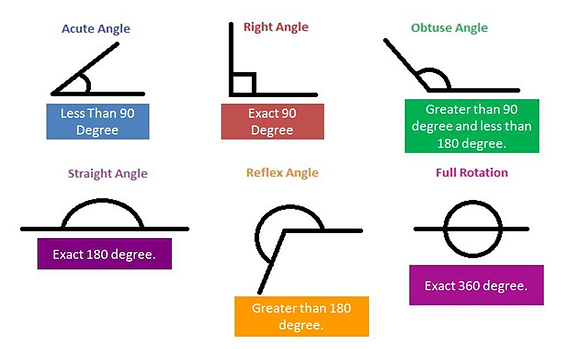
Types of angles
-
Acute Angle
-
Right Angle
-
Obtuse Angle
-
Straight Angle
-
Reflex Angle
-
Full Rotation
Watch and Learn - CLICK HERE

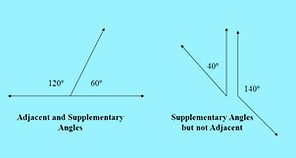
Two angles are complementary if they sum up to 90°.
Two angles are supplementary if they sum up to 180°.
The adjacent angles that are supplementary lead us to a pair of angles that lie on a straight line. This pair of angles are called linear pair of angles.
Watch and Learn - CLICK HERE
Assess yourself - CLICK HERE
Adjacent Angles

Two angles that have a common side and a common vertex is called adjacent angles.
Now observe the next picture in which angles are named ∠1, ∠2 and ∠3. It can be observed that there are two pairs of adjacent angles such as ∠1, ∠2 and ∠2, ∠3.
Then what about the pair of angles ∠1 and ∠3? They are not adjacent because this pair of angles have a common vertex but they do not have a common arm as ∠2 is in between ∠1 and ∠3. Also, interiors of ∠1 and ∠3 do not overlap. Since the pair of angles does not satisfy one among the three conditions, they are not adjacent.

ASSESS YOURSELF

Angles on a straight line

Angles on a straight line sum up to 180°.
In the figure, ∠a+∠b+∠x+∠c = 180°
Assess yourself - CLICK HERE
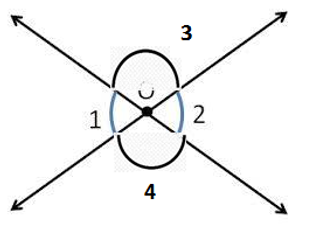
Vertically opposite angles
When two lines intersect each other, two pairs of non-adjacent angles formed are called vertically opposite angles. The angles which are adjacent to ∠1 are ∠2 and ∠4, ∠3 is a non-adjacent angle. Similarly, for the remaining three angles two angles will be adjacent and one angle will be non-adjacent. We can observe that an angle and its non-adjacent angle are just opposite to each other at the point of intersection O (vertex). Such angles which are opposite to each other with reference to the vertex are called vertically opposite angles.
Watch and Learn - CLICK HERE
Assess yourself - CLICK HERE
Transversal
A transversal is a line that intersects two lines at distinct points

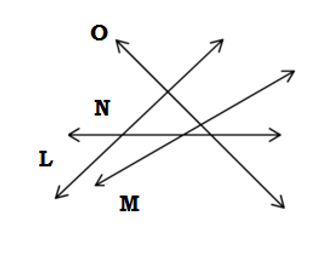
Line O is the transversal of lines L and M, and not the transversal of lines M and N.
Line N is the transversal of lines L and M, and not the transversal of lines M and O.
Line L is not the transversal of lines N and O.
Line M is not the transversal of lines N and O.
Angles formed by a transversal on parallel lines
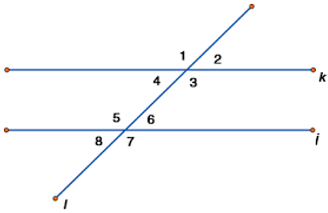
If a transversal meet two lines, eight angles are formed at the points of intersection as shown in the figure.
In Fig, k || j
It is clear that the pairs of angles ∠1, ∠2, ; ∠3, ∠4, ; ∠5, ∠6 and ∠7, ∠8 are linear pairs. Can you find more linear pairs of angles?
The pairs ∠1, ∠3 ; ∠2, ∠4 ; ∠5, ∠7 and ∠6, ∠8 are vertically opposite angles.
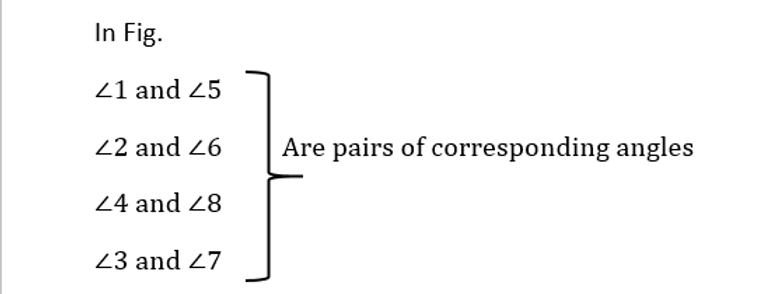
Corresponding angles
All these pairs of angles that have different vertices, lie on the same side (left or right) of the transversal(l), lie above or below the lines k and j. Such pairs are called corresponding angles.
They can easily be identified with ‘F’.
Corresponding angles are equal in parallel lines.
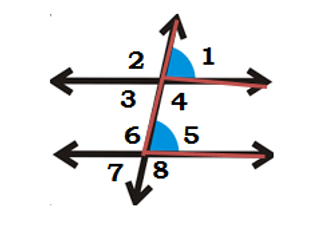
Watch and Learn - CLICK HERE
Alternate interior angles
Alternate interior angles are formed when a transversal passes through two lines. The angles that are formed on opposite sides of the transversal and inside the two lines are alternate interior angles.
They can easily be identified with ‘Z’.
Alternate interior angles are equal in parallel lines.
In the Fig., the pairs ∠3 and ∠5 & ∠4 and ∠6 are pairs of alternate interior angles.

Alternate exterior angles
Alternate Exterior Angles are a pair of angles on the outer side of each of those two lines but on opposite sides of the transversal.
Alternate exterior angles are equal in parallel lines
In the Fig., the pairs ∠1 and ∠7 & ∠2 and ∠8 are pairs of alternate exterior angles.
Watch and Learn - CLICK HERE
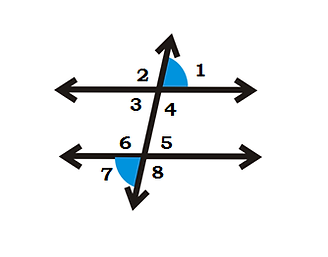
Co-interior angles
Co-interior angles lie between two lines and on the same side of a transversal.
They can easily be identified by ‘U’.
Co-interior angles are supplementary in parallel lines.
Co-exterior angles
Two angles on the same side of the transversal, where two lines are intersected by transversal, outside of the parallel lines
Co-exterior angles are supplementary in parallel lines.

